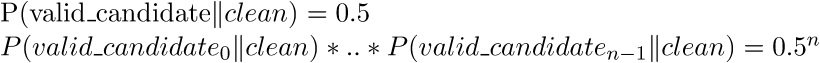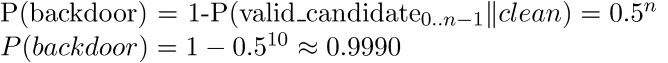While working on some forthcoming research on cryptographic backdoors i came across an interesting asymmetric backdoor designed to subvert RSA key generation algorithms by Ryan Castellucci. The backdoor is particularly interesting because unlike backdoors which subvert key generation by weakening the composite public modulus (eg. choosing prime numbers too close to eachother, choosing a common prime factor with pre-factored moduli, subverting the CSPRNG alltogether, etc.) it is asymmetric in the sense that it can only be used by an attacker posessing theCurve25519 private key corresponding to a Curve25519 public key embedded in the backdoor thus ensuring exclusive access and confidentiality for the attacker. The backdoor embeds an ephemeral Curve25519 public key which is used in conjunction with the attacker’s private key to perform an ECDH key exchange to establish a shared secret with the backdoor which is used as a seed for the prime number PRNG and thus allows PRNG state reconstruction and thus public modulus factorization. The detailed workings of the backdoor are covered by Scratch and Alfonso De Gregorio.
While it does guarantee confidentiality it does not, however, guarantee indistinguishability and as such can be discovered by a third party with blackbox access to a key generation algorithm suspected to be backdoored in this fashion. The reason why it does not guarantee indistinguishability (noted as well by De Gregorio) is because the ephemeral Curve25519 public key embedded in the public modulus of the backdoored RSA public key can be distinguished from a uniform random string. As noted elsewhere Curve25519 points can be distinguished from uniform random strings by virtue of the fact that they lie on the curve. Given a Curve25519 public key, which consists of the 256-bit x-coordinate of an (x,y) point on the curve, the probability that it is an x-coordinate corresponding to a valid curve-point is 1 while for a uniform random string this probability is 0.5. This thus allows for a distinguishing attack on part of a third party collecting npublic keys generated by a blackbox key generation algorithm.
Distinguishing Curve25519 public keys from uniform random strings
Given a 256-bit string we can confirm whether it is a valid x-coordinate to a point on Curve25519 by checking whether evaluating the equation:
Yields a quadratic residue (ie. is congruent to a perfect square modulo the prime field characteristic). We can check whether this is the case by evaluating the equation over the Curve25519 prime field and (since we are dealing with a field of prime characteristic) using theTonelli-Shanks algorithm to obtain its modular square root. If the square of this modular square root equals the equation’s result we know it is congruent to a perfect square and hence x is a valid x-coordinate for a point on the curve. For Curve25519 public keys this will always yield true while for arbitrary 256-bit strings this will only yield true with probability 0.5.
We can use the following python code to perform this check:
from Crypto.Util import number
# Curve25519 is defined over prime field defined by p = 2^255 - 19
CURVE_P = (2**255 - 19)
# Compute Legendre symbol a|p
def legendre_symbol(a, p):
ls = pow(a, (p - 1) / 2, p)
return -1 if ls == p - 1 else ls
# Compute modular square root using Tonelli-Shanks algorithm
# Taken from https://samuelkerr.com/?p=431
def modular_sqrt(a, p):
# Simple cases
if legendre_symbol(a, p) != 1:
return 0
elif a == 0:
return 0
elif p == 2:
return n
elif p % 4 == 3:
return pow(a, (p + 1) / 4, p)
# Partition p-1 to s * 2^e for an odd s (i.e. reduce all the powers of 2 from p-1)
s = p - 1
e = 0
while s % 2 == 0:
s /= 2
e += 1
# Find some 'n' with a legendre symbol n|p = -1.
n = 2
while legendre_symbol(n, p) != -1:
n += 1
# x is a guess of the square root that gets better with each iteration.
# b is the "fudge factor"
# g is used for successive powers of n to update both a and b
# r is the exponent - decreases with each update
x = pow(a, (s + 1) / 2, p)
b = pow(a, s, p)
g = pow(n, s, p)
r = e
while True:
t = b
m = 0
for m in xrange(r):
if t == 1:
break
t = pow(t, 2, p)
if m == 0:
return x
gs = pow(g, 2 ** (r - m - 1), p)
g = (gs * gs) % p
x = (x * gs) % p
b = (b * g) % p
r = m
# Evaluate curve over candidate x-coordinate
def do_curve(x):
return ((x**3 + 486662*(x**2) + x) % CURVE_P)
# Determines whether a candidate x-coordinate belongs to a valid point (x,y) on Curve25519
def is_on_curve(x_candidate):
x = number.bytes_to_long(x_candidate[::-1])
y2 = do_curve(x)
y = modular_sqrt(y2, CURVE_P)
return ((y**2 % CURVE_P) == y2)Determining backdoor presence
We can use this fact to determine the presence of this particular backdoor as follows. Consider we have n public keys generated by a suspicious key generation algorithm. From each of those public keys we will extract a candidate ephemeral Curve25519 public key from the RSA public modulus. If any of these candidate keys proves not to be a valid curve x-coordinate we can rule out the presence of the backdoor with certainty (since all embedded public keys are valid coordinates). If, however, all candidate keys are valid curve x-coordinates we are either dealing with the backdoor or with a (statistical anomaly of a) ‘clean’ key generation algorithm. For the latter case we have the conditional probability:
Hence if we collect n = 10 RSA public keys from a suspect key generation algorithm and all of them pass the curve test the probality they were not generated as the result of a statistical anomaly on part of a clean algorithm is:
Which seems sufficient to rule out statistical anomalies with some confidence.
Demonstration
I have uploaded Castellucci’s backdoor script, my backdoor detecton script and several test certificates (those starting with the prefix poc are generated by the backdoor, those with the prefixclean by openssl) here. When executed it looks like this:
$python detectbd.py poc
[+]RSA public keys generated by backdoor with probability 0.999023
$python detectbd.py clean
[+]RSA public keys generated by backdoor with probability 0.000000Backdoor improvements
An improvement to Castellucci’s backdoor design was offered by De Gregorio offering confidentiality, indistinguishability and forward secrecy properties among others and his HITB talk whitepaper is worth checking out.
Source:https://samvartaka.github.io/

He is a well-known expert in mobile security and malware analysis. He studied Computer Science at NYU and started working as a cyber security analyst in 2003. He is actively working as an anti-malware expert. He also worked for security companies like Kaspersky Lab. His everyday job includes researching about new malware and cyber security incidents. Also he has deep level of knowledge in mobile security and mobile vulnerabilities.