A group of Chinese researchers have just released a paper in which they make the claim that they are capable of breaking 2048-bit RSA, despite the fact that they have not yet done so. It is important to treat this matter seriously. It’s possible that it’s incorrect, but there’s no denying that it’s not right.
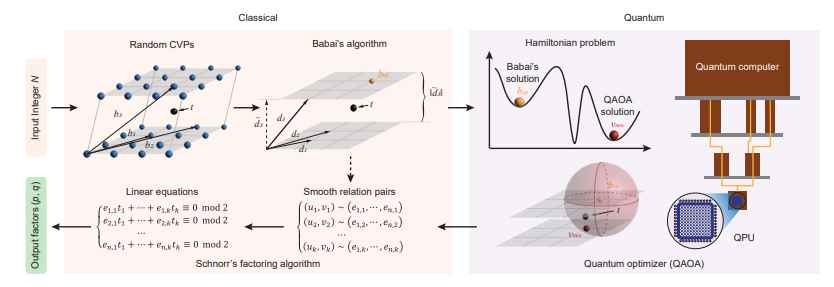
Because of Shor’s algorithm, we have known for a long time that factoring on a quantum computer is a simple process. However, in order to factor anything that even somewhat resembles the key sizes that are in use today, a massive quantum computer with millions of qbits is required. The researchers have accomplished what they were out to achieve by combining traditional methods of lattice reduction factoring with an algorithm for quantum approximation optimization. This indicates that all they want is a quantum computer with a capacity of 372 qbits, which is well within the realm of what is feasible in the present day.
If 2048-bit RSA could be broken, or in other words, if there was a mechanism that could reliably and rapidly identify the secret prime numbers that underlie the algorithm, this would be an enormously major accomplishment. Although the RSA algorithm has been largely superseded in consumer-facing protocols such as Transport Layer Security, it is still widely used in older enterprise and operational technology software as well as in many code-signing certificates. This is due to the fact that many code-signing certificates require it.
If a malicious adversary were capable of generating these signing keys or decrypting the messages that are protected by RSA, then that adversary would be able to snoop on internet traffic as well as potentially pass off malicious code as if it were a legitimate software update, which would potentially enable them to seize control of third-party devices. If an adversary were capable of generating these signing keys or decrypting the messages that are protected by RSA, then that adversary would be able to s
The research explains how a device with just 10 superconducting qubits was able to break a key with a length of 48 bits for the first time ever. In order to decrypt an RSA-2048 key, you will need no more than 400 qubits, which is already within the realm of possibility for present technology.

It is common knowledge that using a quantum computer and Shor’s quantum algorithm, one can quickly and easily decompose (factorize) large numbers into prime factors and, as a result, decrypt a key or a message much more quickly than using a classical computer. This is possible because of the quantum computer’s ability to process information at an atomic level. The primary drawback of using Shor’s technique is that factoring cryptographically relevant long keys requires quantum computers with hundreds of thousands or perhaps millions of qubits. This makes it impractical to use the algorithm.
Since Peter Shor’s technique became public knowledge, researchers have been attempting to improve upon it by scaling it up. Their goal is to make RSA cracking less resource demanding for quantum computers. Alexei Kitaev, a Russian scientist, was the one who first suggested one of the potential solutions to this problem. In 2016, a team of physicists from the Massachusetts Institute of Technology and the University of Innsbruck developed a quantum computer that, when it was used to execute Shor’s algorithm, provided proof that the scaling was correct. However, this was not sufficient to make a significant advancement.
The quantum system that Chinese scientists had was quite simple, but they intended to improve it. They followed the recommendation of a different cryptographer named Klaus-Peter Schnorr, who had suggested a method in the spring of last year that greatly accelerates the factorization process.
The work of Schnorr was attacked by industry professionals who believed it was incapable of withstanding scaling up to cracking large keys. The “death” of long keys might “truly end the tale” about RSA encryption. The Chinese researchers say that they have discovered a solution around this constraint and that they have proven it in reality by breaking a 48-bit key using a 10-qubit quantum machine. They also claim that the approach works for cracking keys of a cryptographically relevant length.
In point of fact, Chinese researchers have integrated traditional techniques of lattice reduction factorization with an algorithm for quantum approximate optimization (QAOA). Only 372 qubits would be enough, according to their estimates, in order to decrypt an RSA-2048 key. For instance, IBM will soon have a system that is quite comparable to it. There are 433 qubits available for use with the IBM Osprey processor. If the claims made by Chinese scientists are true, then it won’t be more than a few of years until quantum computers break the RSA-2048 encryption standard.

Information security specialist, currently working as risk infrastructure specialist & investigator.
15 years of experience in risk and control process, security audit support, business continuity design and support, workgroup management and information security standards.